what happens to a discount bond as the time to maturity decreases
Theoretical Economics Letters
Vol.iv No.v(2014), Article ID:46608,8 pages DOI:ten.4236/tel.2014.45043
The Fourth dimension Decay of Bond Premium and Discount—An Analysis of the Fourth dimension Passage Effect on Bond Prices
Jorge Brusa1, Jenny Gutwo*, Grace Yaru Liu3
iDivision of International Banking & Finance Studies, Sanchez School of Business, Texas A&M International University, Laredo, USA
2College of Business, Academy of Dallas, Irving, USA
3Department of Supply Chain and Information Systems, Pennsylvania State University, University Park, USA
E-mail: jbrusa@tamiu.edu, *jgu@udallas.edu, ygl100@psu.edu
Copyright © 2014 past authors and Scientific Enquiry Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC Past).
http://creativecommons.org/licenses/by/4.0/



Received 25 April 2014; revised xx May 2014; accepted 30 May 2014
Abstract
In this paper, we show that the toll of a premium bail and the price of a disbelieve bail will both motility toward face value at an increasing rate as the bonds approach maturity. Nosotros nowadays a mathematical proof to bear witness that the decline in premium and discount decline over fourth dimension, to exist referred to as time decay, accelerates as fourth dimension passes by. We also provide numerical examples and graphical representations to illustrate the time passage effect on bond prices and hash out the implications of the findings to bail investor and asset managers in low-cal of the quantitative easing policies taken past central banks afterwards the 2008 financial crunch.
Keywords
Time Decay, Premium Bond, Discount Bond, Time Passage Effect, Quantitative Easing

one. Introduction
Researchers in economic science and finance have studied the relationships among bond prices, interest rates, and maturity for many years. 1 of the all-time known results in the written report is that, if the marketplace involvement rate on a bail remains unchanged, the price of a bond will approach its confront value as the bond approaches maturity. However, how exactly and in what way the bail price approaches its face value has not been well discussed in textbooks. For example, when a bond is selling at premium (i.e. when the bond price is to a higher place its face value), the only way for the bond price to approach its face value is to move downward. Therefore the price path toward maturity for a premium bond must be downward-sloping. Notwithstanding, a downward-sloping path could be convex (decreasing at a decreasing rate), concave (decreasing at an increasing rate), or a straight line (decreasing at constant rate), to proper noun just 3. Similarly, when a bail is selling at disbelieve (i.e. when the bond cost is below its face value), the only manner for the bond price to reach its face value is to move upwards. Therefore the price path toward maturity for a discount bond must be upward-sloping. Even so, an upwards-sloping path could as well be convex (increasing at an increasing rate), concave (increasing at a decreasing charge per unit), or a directly line (increasing at constant rate).
In this paper we formally nowadays a mathematical proof to show that the toll path for a premium bond is concave (decreasing toward the par at an increasing rate) and the price path for a disbelieve bond is convex (increasing toward the par at an increasing rate) as the bond approaches maturity. In other words, we show that both the premium (defined every bit price minus the par) and the discount (divers as par minus the price) are diminishing at an increasing charge per unit equally the bond approaches maturity. This is the showtime contribution of our study because, to the best of our knowledge, no report in the literature has formally presented a mathematical proof to show that both the premium and the disbelieve diminish at an increasing rate as bail approaches maturity1. Since both the premium and the disbelieve will decrease over time when interest rate remains unchanged, we will refer to the subtract in premium and discount as fourth dimension decay of premium and disbelieve.
Ane of the reasons that almost textbooks only briefly address the event of bond price path toward maturity (east.g. Brigham and Houston, 2012) [ane] and that some books do not fifty-fifty mention the issue (e.m. Berth, Cleary, and Drake, 2014; Gitman, Joehnk, Smart, 2011; Keown, Martin, and Piddling, 2014) [ii] -[four] may be that, in guild to examine the time passage effect on bond price, the condition that the interest rate remains unchanged must agree. Some authors consider that condition too stiff and therefore practically impossible2. It is truthful that involvement rate may exist constantly changing. However, the change in involvement rate should not the reason to restrain united states of america from examining the price modify due to time passage. As Fabozzi (2007) [v] indicates, the change in bond price tin can always be decomposed into 2 components: one component due to time passage toward maturity without any change in interest rate, and 1 component due to the modify in interest rate. In other words, regardless of whether interest rate changes or remains abiding, at that place is always a component of change in bail prices due to time passage and that component should be thoroughly examined and fully understood3. This is the second reason that nosotros thoroughly examine how fourth dimension passage affects bail prices.
The results of this study should be interesting not only to scholars studying fixed income securities, but also to asset managers with clients holding bonds. Every bit nosotros bear witness in Sections ii and iii in the paper, for premium bonds, their value decreases toward the par at an increasing rate over time. The quantitative easing policies initiated by the Federal Reserve, Banking concern of England, European Key Banking company, and Bank of Japan equally a response to the 2008 financial crunch take driven the global interest rates to historical lows. As a issue, most bonds issued prior to 2008 (which usually deport coupon rates higher than the current interest rates), have become premium bonds in the past few years. As these bonds approach maturity, their prices will move lower over time fifty-fifty as the central banks continue to maintain the interest rate at the current level. Furthermore, since the prices of these premium bonds decrease at an increasing rate, the subtract in value for these bonds volition advance as they approach maturity in the next few years. As many individual bond investors do not understand the time passage effect on bond prices, nugget managers with clients investing in private bonds or bond funds are likely to be questioned past their customer as the clients encounter the value of their bonds declining at an increasing rate. The analyses of the bond toll path volition provide to asset managers a tool to explain to their clients why the value of these bonds declines over time. This is the third reason for the report.
The residuum of the paper is organized as follows. In Department two, we nowadays a mathematical proof to show how both the premium and the disbelieve will subtract at an increasing rate as the bond approaches maturity. In Section 3, we nowadays numerical examples to illustrate our findings. In Section 4 we talk over the implications of the findings in the paper. Nosotros conclude the paper in Section 5.
ii. Mathematical Model
In this section, we will present a mathematical proof to show that the price of a premium bond will decline toward confront value at an increasing rate over time, and the price of a discount bond volition ascension toward confront value, likewise at an increasing rate as it approaches maturity.
The way nosotros evidence the arguments is as follows: we volition first bear witness that the toll of a premium bond increases at a decreasing rate as the bail's term to maturity increases. However, in exercise, a bond's term to maturity decreases over time. Consequently, every bit a bond approaches maturity, the price of a premium decreases at an increasing charge per unit. Similarly, for a discount bail nosotros will show that as term to maturity increases, the price decreases at a decreasing rate. Therefore, as the bond approaches the maturity and the term to maturity decreases, the cost of a disbelieve bond increases at an increasing rate.
We now formally present the mathematical proof:
Let T be the term to maturity of the bail (and thus T decreases when a bond moves toward maturity as time passes by), cr be the coupon charge per unit, i be the marketplace rate of interest, and F exist the face (par) value of the bond. Then the price of the bond, P, is determined past the equation:
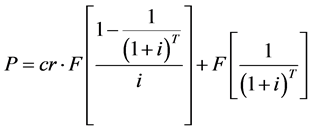
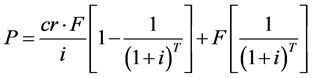 (1)
(1)
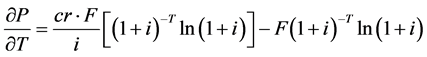
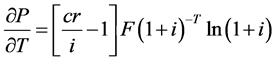 (ii)
(ii)
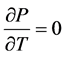 if
if 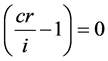 (for a par bond where cr = i) (3)
(for a par bond where cr = i) (3)
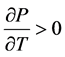 if
if 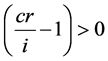 (for a premium bail where cr > i) (4)
(for a premium bail where cr > i) (4)
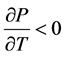 if
if 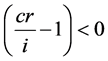 (for a discount bond where cr < i) (5)
(for a discount bond where cr < i) (5)
Equation (3) shows that for a par bond, the cost is a abiding (equal to the par value), and the bond price path toward maturity for a par bond is a horizontal directly line.
Equation (four) shows that for a premium bail, the cost is an increasing office of its term to maturity. As the bond approaches maturity, the term to maturity T decreases. Consequently, the price for a premium bond decreases as information technology approaches maturity.
Equation (5) shows that for a discount bond, the price is a decreasing function of term to maturity. As a bail approaches maturity, the term to maturity T decreases. Equally a result, the price for a discount bond increases as it approaches maturity.
To find out whether the bond toll path for a premium bond is decreasing at an increasing charge per unit or at a decreasing rate, and whether the bond price path for a discount bail is increasing at an increasing rate or at a decreasing rate, nosotros differentiate Equation (two) with respect to T again and obtain:
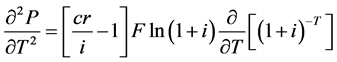
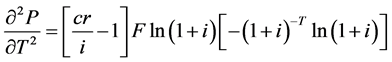
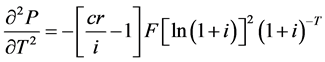
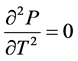 if
if 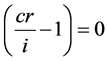 (for a par bond) (vi)
(for a par bond) (vi)
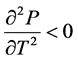 if
if 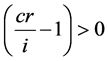 (for a premium bond) (7)
(for a premium bond) (7)
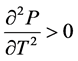 if
if 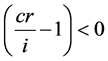 (for a discount bond) (8)
(for a discount bond) (8)
Combining Equations (4) and (vii), the results evidence that the price for a premium bond is an increasing function with respect to T at a decreasing rate. Yet, as a bond approaches maturity, the term to maturity T decreases. Therefore, the toll path for a premium bail toward maturity is decreasing at an increasing rate.
Equation (v) suggests that the toll of a discount bond is a decreasing function of T. Yet, Equation (8) suggests that the downward-sloping curve becomes less negative as T increases. Therefore Equations (5) and (8) suggest that the cost for a discount bail is decreasing with respect to T at a decreasing rate. However, equally a bond approaches maturity, the term to maturity T decreases. Therefore, the toll path for a discount bail toward maturity is increasing at an increasing rate.
In the adjacent section, nosotros provide a few numerical examples and graphical representations to illustrate the mathematical proofs.
3. Numerical Illustrations
In Table ane nosotros present the prices for bonds with a face value of $1000, five different coupon rates: 12%, 10%, 8%, half-dozen%, and 4%; and 21 unlike terms to maturity from 0 to 20 years. We assume the market charge per unit of interest to be 8%, and coupon payments are fabricated annually.
In the tabular array, we can detect the prices for premium bonds (bonds with coupon rates of 12% and x%) are increasing functions of term to maturity at a decreasing rate. For example, for the 12% bond the cost increases past $37.04 when term to maturity increases from 0 to 1 year, but the cost increases by only $8.59 when the term to maturity increases from 19 to twenty years. Since the cost is increasing at a decreasing rate, it would non increase indefinitely as term to maturity approaches infinity. The price is equal to 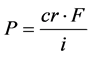 equally T approaches infinity
equally T approaches infinity
(known as a perpetual bail) according to Equation (1), or $1500 for a 12% bond when the market rate of interest is 8%. Figure 1 is the graphical representation of Table ane, showing bond prices as a function of term to maturity.
Since the price for a premium bond increases at a decreasing rate as term to maturity increases, the price path toward maturity engagement, which is the price movement with a decrease in term to maturity, is decreasing with an increasing rate.
Similarly, the prices for discount bonds (bonds with coupon rates of 6% and 4%) are decreasing functions of term to maturity at a decreasing rate. For case, for the iv% bail the price decreases past $37.04 when term to maturity increases from 0 to ane year, simply the toll decreases past only $8.59 when the term to maturity increases from 19 to 20 years. Since the price is decreasing at a decreasing charge per unit, it does not decrease indefinitely equally term to maturity approaches infinity. The price for a perpetual discount bail (with term to maturity approaches to in

Tabular array 1. The prices for bonds with a face value of $thousand, coupon rates of 12%, 10%, 8%, 6%, and 4% respectively (bold annual payment), and terms to maturity from 0 to twenty years when the market rate of interest is eight%.
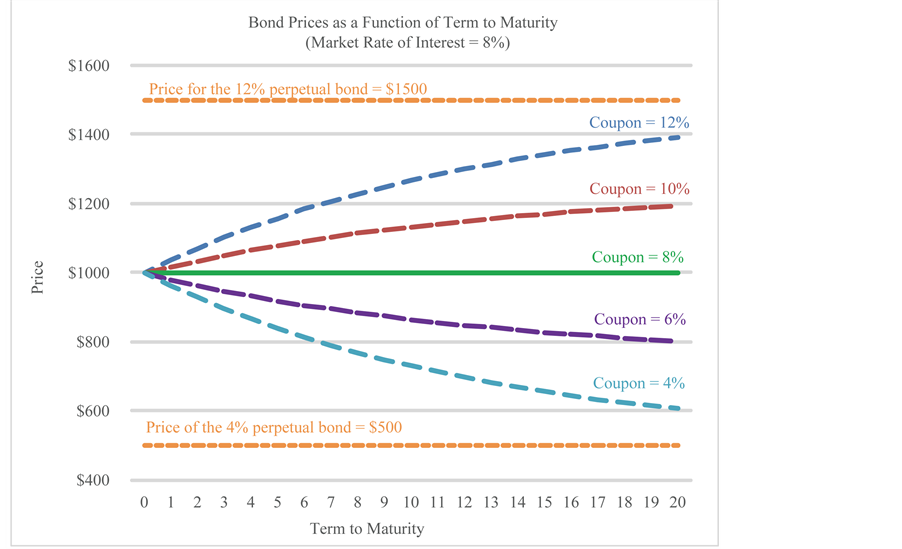
Figure ane. Bond prices as a role of term to maturity: the face value is $one thousand, coupon rates are 12%, 10%, viii%, 6%, and 4% respectively (assuming annual payment), and terms to maturity are from 0 to xx years when the market charge per unit of interest is viii%.
finity) is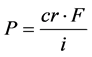 , co-ordinate to Equation (1), or $500 for a 4% bond when the market place rate of involvement is 8%.
, co-ordinate to Equation (1), or $500 for a 4% bond when the market place rate of involvement is 8%.
Since the price for a discount bail decreases at a decreasing rate equally term to maturity increases, the toll path toward maturity date, which is the price movement with a subtract in term to maturity, is increasing with an increasing charge per unit.
To enhance the understanding of the effect of fourth dimension passage on bond prices, nosotros construct Tabular array 2 to illustrate how the prices of twenty-year bonds with different coupon rates converge toward face value as fourth dimension approaches maturity engagement.
The results in Tabular array 2 show that the price for the ten% premium bond declines past $iv.29 from $1196.36 to $1192.07 in the outset year after it is issued (from 20 years remaining until maturity to 19 years remaining until maturity). However, during the very last year immediately before maturity (from one year remaining until maturity to the maturity date), the price declines by $18.52 from $1018.52 to $1000. The results show the toll path toward maturity for a premium bond decreases at an increasing rate.
Every bit the bond approaches maturity, the price approaches the confront value and the premium (defined every bit the dollar amount higher up the face value) declines purely due to time passage without any change in interest rate, we refer to the reject equally time decay in bond premium.
Similarly, the results in Tabular array 2 show that, the price for the six% premium bail rises past $iv.29 from $803.64 to $807.93 in the first year after it is issued (from 20 years remaining until maturity to 19 years remaining until maturity). However, during the very concluding year right before maturity (from one year remaining until maturity to the maturity date), the cost rises by $xviii.52 from $981.48 to $1000. The results testify the price path toward maturity for a disbelieve bond rises at an increasing rate.

Table ii. The convergence of bail prices toward face up value as they approaches maturity date. The bonds accept coupon rates of 12%, 10%, eight%, vi%, and four% respectively and a confront value of $grand. Nosotros assume all the bonds start with an initial term to maturity of 20 years, the market rate of interest is viii%, and interests are paid annually.
As the bond approaches maturity, the cost approaches the face value and the disbelieve (defined every bit the dollar amount below the face value) declines purely due to time passage without any change in involvement charge per unit, we refer to the refuse as fourth dimension decay in bond discount.
Figure 2 is the graphical representation of Tabular array 2 showing the price path of bonds with different coupon rates as these bonds approach maturity when all the bonds start with an initial term to maturity of xx years. Note that the bail prices in Effigy i and the bail prices in Figure two are symmetric with respect to the y-axis as the x-axis in Figure one is the term to maturity (number of years in ascending club) while the 10-centrality in Figure 2 is the term remaining until maturity (number of years in descending order).
4. Implications of the Findings
The findings in the paper in and by itself are interesting and important. As we discussed, the change in bond prices tin can always be decomposed into at least 2 components: one component due to fourth dimension passage without taking into account the modify in involvement rate, and one component due to the alter in interest charge per unit. To fully understand bail pricing, information technology is necessary to empathize the driving forces behind both components. The findings in this paper contribute to the understanding of the first component.
Moreover, the findings in the paper can likewise enhance the management of fixed income securities and the advice between asset managers and their clients. As we take shown in the paper, the value of premium bonds declines at an increasing charge per unit as they arroyo maturity. To answer to the 2008 financial crunch, central banks worldwide take taken programs in the past few years. These programs have driven interest rates to historical lows and many bonds issued before 2008 (which deport coupon rates higher than the current interest rates) have become premium bonds. Equally these bonds approach maturity in the next few years, their value will turn down. Moreover, because the price of premium bonds declines at an increasing rate, the pass up of these bonds' value volition advance fifty-fifty central banks maintain the current policy unchanged. Equally nearly investors do not fully understand the time decay of bond premium, they may unfairly blame asset managers for the reject in bond value even the decline is purely due to the passage of time and the central banks' monetary policies. A better understanding of the price path event on bond prices will assistance asset managers manage bond portfolios more than effectively and enhance the communications between asset managing director and their clients.
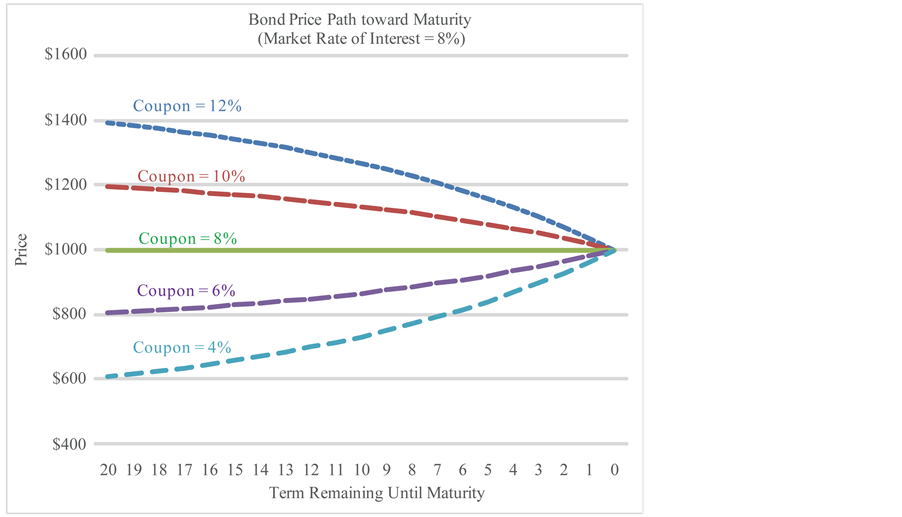
Effigy 2. Bail prices as a function of term remaining until maturity: the face up value is $1000, coupon rates are 12%, 10%, viii%, six%, and 4% respectively (assuming annual payment), and all the bonds start with an initial term to maturity of 20 years when the market rate of interest is eight%.
5. Conclusion
In this paper, we show that every bit bonds approach maturity, the price of a premium bond will decline to the face value at an increasing rate, and the price of a disbelieve bond volition rise to the face value at an increasing rate. As both the prices of premium and discount bonds motility toward face value, the premium and the discount volition decrease over time fifty-fifty when interest rate remains unchanged. We refer to the subtract purely caused past fourth dimension passage every bit time decay in premium and discount. We nowadays a mathematical proof to show that the time decay accelerates over time. We too provide numerical examples and graphical representations to illustrate the fourth dimension passage effect on bail prices. Finally we discuss the implications of the findings to bond investors and nugget managers.
References
- Brigham, Eastward. and Houston, J. (2012) Fundamentals of Financial Direction. 7th Edition, South-Western Cengage, Boston.
- Berth, L., Cleary, S. and Drake, P. (2014) Corporate Finance. John Wiley & Sons, Hoboken.
- Gitman, L., Joehnk, Thou. and Smart, S. (2011) Fundamentals of Investing. 11th Edition, Prentice Hall, Upper Saddle River.
- Keown, A., Martin, J. and Petty, W. (2014) Foundation of Finance. eighth Edition, Pearson, London.
- Fabozzi, F. (2007) Stock-still Income Assay. second Edition, Wiley, Hoboken.
- Sharpe, W., Alexander, G. and Bailey, J. (1998) Investments. sixth Edition, Prentice Hall, Upper Saddle River.
- Lasher, W. (2014) Applied Financial Management. seventh Edition, Cengage Learning, Boston.
- Merton, R. (1973) Theory of Rational Option Pricing. The Bell Periodical of Economics and Direction Science, iv, 141-183. http://dx.doi.org/10.2307/3003143
NOTES

*Corresponding author.

oneWe examined more than xxx textbooks in investments, financial management, and fixed income securities. The just textbook that briefly addresses the second derivative of the time path of bond prices—which is the major focus of our paper—is Sharpe, Alexander, and Bailey (1998) . However, the volume has not been in impress since 1998. Also the book did not present a mathematical proof to examine the relationship between fourth dimension passage and bond prices although information technology gave a numerical illustration. Since the book was published before the 2008 financial crisis, it did not accost how the time passage effect on bond toll may affect portfolio managers under the current fundamental banks' quantitative easing (QE) programs, which is another topic nosotros address in our paper.
2For instance, one author starts the word of this outcome past saying:
"Let'south imagine a very unlikely upshot just to enhance our understanding of the procedure involved in bond pricing. What would happen to the cost of the… bond as time goes by if involvement rates didn't modify again for the remainder of the bond'south life (a practical impossibility)?" (Lasher 2014, p. 299)
3A similar phenomenon can found in study of option pricing. Merely as bond prices are affected by passage of time and market place rate of interest, choice prices are besides affected by passage of fourth dimension and the underlying asset price. Even though the underlying asset price is constantly changing only like the marketplace charge per unit of interest, how choice prices are affected by the passage of fourth dimension while holding the underlying nugget cost abiding is very thoroughly studied and well understood in the selection pricing theory. For the details of how pick prices are bear on by the passage of time, known as time decay of option prices, come across Merton (1973) and Smith (1976) .
Source: https://www.scirp.org/html/2-1500558_46608.htm#:~:text=Similarly%2C%20for%20a%20discount%20bond,increases%20at%20an%20increasing%20rate.
0 Response to "what happens to a discount bond as the time to maturity decreases"
Post a Comment